++ 50 ++ 理科 体積 の 求め �� 132181-面積 体積 公式 一覧 小学生
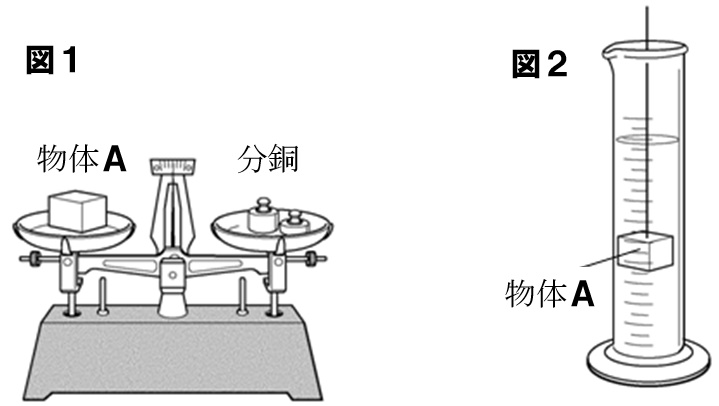
プラスチックのコップ,受け皿(プリンカップなど),メスシリンダー,調べるもの 図のように,受け皿の中にプラスチックのコップ を入れ,コップに水をぎりぎりまで入れる。 調べるものを水の中にしずかに入れる。 受け皿にあふれた水をメスシリンダーに入れて, りょうをはかる。 ★ ものを水にしずめたときにふえた水のりょうが, そのものの体積だよ! 1 2 3 じゅんび アルキメデスと金の 90(g)÷ 15(g/cm 3 ) = 60(cm3) 以上、『密度の公式 – 物質の密度の求め方は「しみた」の法則』を紹介しました。 密度の公式は、密度・質量・体積 からなっています。 密度の単位である『g/cm 3 』を知っていれば自然と計算式が出てきますね。 また = 質量 ÷体積 = 1000÷111 = 9001 だいたい密度が9 g/cm³ってことがわかった。 このとき、 「この延べ棒はぜんぶ金でできてないじゃないか! 」 ってだまされずに気づくことができるんだ。 なぜなら、 金の密度は1932 g/cm³ になるはずだからね。 物質によって密度が違うから、すぐに金じゃないって気づくことができるね。 あぶねえあぶねえ。 ちなみに、密度がだいたい9
中学理科 密度の定期テスト予想問題 Pikuu
面積 体積 公式 一覧 小学生
面積 体積 公式 一覧 小学生- 算数では水の体積から重さを表せるようになればばっちりです。 ・算数で習う水槽の中の水の体積と重さの関係を理解して単位変換できるようにしよう いびつな形の体積が求められるようになろう。 いびつな形の体積を直接求めるのはとても難しいもの q ガンダムの体積の求め方を答えなさい。 って出たら。 こう答えるのだ。 ①ガンダムの頭に穴を開ける。 ②そこに水を入れて、満タンにする。 (アムロのことは気にしなくてよい。) ③どこからでもいいから、頭に開けた穴と同じ大きさの穴を開けて。




密度の計算と 溺れないためにできること Menon Network
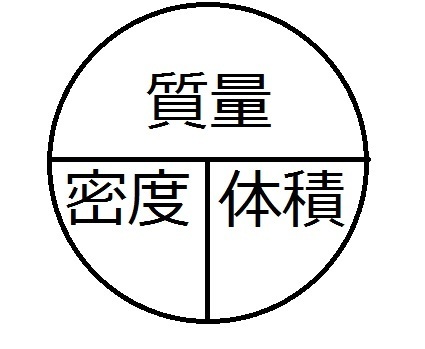
体積=質量÷密度で算定できます。 最後に、密度を隠すと「質量÷体積」が残ります。 質量、体積、密度を求める公式を下記に示します。 質量 (g)=体積 (cm 3 )×密度 (g/cm 3) 体積 (cm 3 )=質量 (g)÷密度 (g/cm 3) 密度 (g/cm 3 )=質量 (g)÷体積 (cm 3) 下図をみてください。 質量が100kgのコンクリートがあります。 体積を計算しましょう。 なおコンクリートの密度は23g/cm 3 とします。 体積=質 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle 正三角形の面積について復習したい方はこちらも参照してください。 3分で分かる! 正三角形の面積の求め方・公式をわかりやすく もう一つ正四面体の体積の求め方を示しておきたいと思います。 それは正四面体に外接する立方体に着目し
四角柱、円柱の体積の考え方 柱と錐で体積の計算方法が変わってくるので、まずは、四角柱、円柱の体積について解説していきます。 まずは前回の直方体の復習をしてみましょう。 体積とは 平面の図形をどれだけ「高さ」の方向に積み重ねたか で考え 球の体積、表面積の求め方例題 例題半径が2㎝の球について、体積と表面積を求めなさい。 半径が2㎝ということから、 となります。 これを公式に代入して計算していけばOKです。 体積 表面積 ゆい 公式を覚えてしまえば 計算はラク 直方体と立方体の体積の求め方です。 求め方は難しいものではありませんが、正確に計算できるように練習してください。 複雑な体積の求め方や単位についてもしっかり学習しましょう。 直方体の体積 直方体の体積=たて×横×高さ 立方体の体積
体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。立方体の体積は (1辺)×(1辺)×(1辺) で求めることができます。 だけど、これは直方体の (たて)×(よこ)×(高さ) これと全く同じものです。 全ての辺が同じ長さになってしまう立方体では、辺の区別をつけず たて、よこ、高さのそれぞれを テーマ: 理科 前回は、濃度とその計算と求め方について行いました。 濃度の意味から数式まで難しくみえますが、一つ一つ意味を知ればそこまでハードルは高くないと思います。 今回は体積・重さ・密度について行います。 一気にする




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ
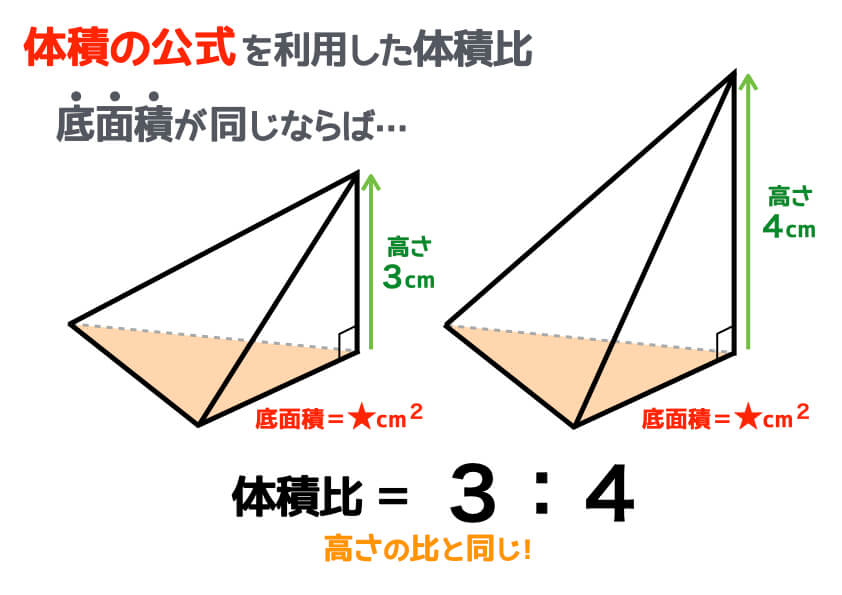



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ
の体積 V = abh V = a b h 体積 = たて × 横 × 高さ 柱体の体積 柱の体積は、 底面積 ていめんせき S S 、高さ h h として、次の式で求められます。 この公式は、 底面 ていめん の形によりません。 柱体 ちゅうたい の体積 V = Sh V = S h 体積 = 底面積 × 高さ 角柱と円柱の図を、それぞれ見てみましょう。 角柱の体積 底面積 S、高さ h の 三角柱 さんかくちゅう 三角柱や四角柱などの体積は、底面積 S S四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 体積の求め方、覚え方 前述した体積の公式を使って、具体的に各図形の体積を計算します。 立方体の体積 下図が立方体です。立方体は全ての辺が同じ長さなので、体積の計算も簡単です。積分式: V=8 ∫∫ (1-X2-Y2)1/2 dXdY (8分の1球の体積X8) 上記の積分式は、 体積を求める数値積分のベースにはなりますが、 解析的 に計 算するのは容易ではありません。 そのため、最初に説明したように 回転体 の体積 を求めるやり方で計算してみ
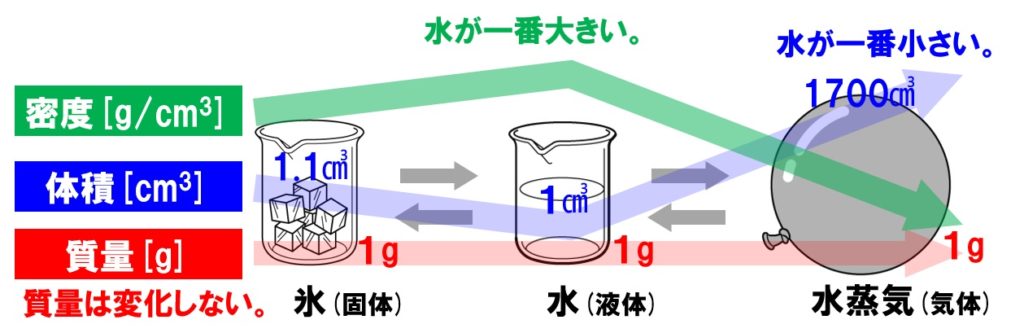



中1理科 状態変化と質量 体積 密度のポイント Examee




中1理科 密度の単位と計算方法 練習編1 映像授業のtry It トライイット
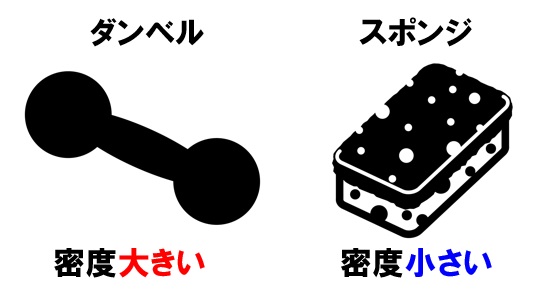
体積 = 一辺 × 一辺 × 一辺 V = a 3 2 直方体の体積 三辺の長さが a,b,h の直方体の体積 V は、次の式で求められます。 縦:a 横:b 高さ:h 体積 = 縦 × 横 × 高さ V = a b h 3 柱体の体積 柱体の体積は、底面積 をS、高さを h として、次の式で求められます。 底面積:S 高さ:h 体積 = 底面積 × 高さ V = S h 4 角柱の体積 三角柱や四角柱などの体積は、底面積を S、高さを h として、次の式 三角柱の体積の考え方 「柱」と「錐」で体積の計算方法が変わってくるので、まずは、三角柱の体積について解説していきます。 まずは前回の直方体の復習をしてみましょう。 体積とは 平面の図形をどれだけ「高さ」の方向に積み重ねたか で考えました。 よって、密度が大きい材料である鉄などの金属はサイズが小さくても重く感じ、パンなどの密度が低いものはサイズが大きくても軽いと感じるわけです。 なお、 密度、質量、体積の中で二つがわかっていれば残り一つを計算することができます。 例えば



密度の求め方 小中学生の学習に役立つ記事がたくさん




密度の計算習得は し た み これだけ 土星は水にうく 理科のすゝめ 高校受験 大学受験向け
これだけの質量の差があるので、 両者を同じ質量にすると、体積は木材の方がずいぶんと大きくなってしまう わけです。 このような、物の「 単位体積( 1 ㎤ や 1 ㎥ など )あたりの質量( g , kg ) 」を「 密度 」と言います。 密度の単位 は「 g/㎤ ( グラム 浮力はどうやって求めるのか? 中学理科の浮力と水圧との関係、浮力が発生する仕組みをわかりやすく解説します。 目次本記事の内容 1浮力を理解するためにおさえる3つのポイント;体積の求め方 質量と密度から体積を求めるには、 体積=質量÷密度 という公式を使います。 例えば、質量が 10 g で、密度が 2 g / c m 3 であるような物体の体積は、 10 ÷ 2 = 5 c m 3 になります。 3つの公式の覚え方 質量=体積×密度 密度=質量÷体積 体積=質量÷密度 という3つの公式は、まとめて1つの図で表すことができます。 3つの領域のうち、求めたいものを隠せば公式が得られます。 例え
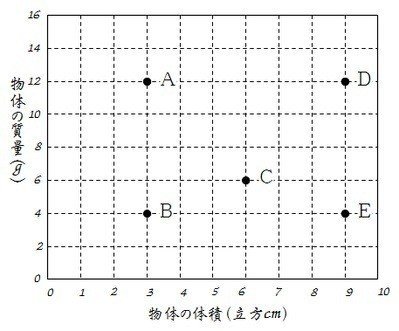



物質の密度 Shun Ei Note



1
球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 4 3 π r 3 になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 たとえば、半径30 cmのサッカーボールがあったとしよう。 こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、 ³ 4 3 × π × 30 × 30 × 30立体切断⑶ 体積 16 ⑴ FKの長さを求めなさい。 ⑵ HNの長さを求めなさい。 ⑶ FLの長さを求めなさい。 ⑷ HMの長さを求めなさい。 ⑸ 立方体の2つに分けられた部分のうち、小さい方の体積を求めな実は,面積が定積分で計算できたように, 体積も定積分 によって計算できます。 立体の断面積S (x)を,aからbの区間で定積分する と,aからbまでの立体の体積を求めることができるのです。 POINT 面積を積分すると,体積になる のですね。 体積の求め方∫ ab S (x)dx を使って,実際に問題1,問題2を解いていきましょう。 この授業の先生 浅見 尚 先生 センター試験数学から難関大理系数学まで幅
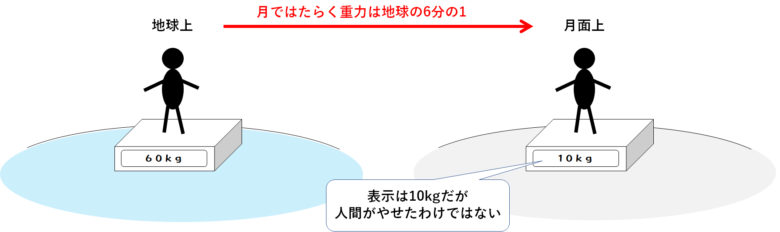



中1化学 質量と重さ 体積 中学理科 ポイントまとめと整理




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
・水に溶けない固形のものなら,水を入れたメスシリンダーに沈めて,推移の上昇した分が,その固体の体積です。 密度が分かっている物質なら, (密度)= (質量)÷ (体積) ですから, (質量)= (密度)× (体積) (体積)= (質量)÷ (密度) で求まります。 この3量関係は重要です。 (密度)= (質量)÷ (体積)を覚えて, 自分で計算してあと2式を導きだせるようにしましょう。 14人 がナイス! していこれは、4辺の高さがバラバラなので、 平均の考え方を使って、 こういう直方体に直すとやりやすいね。 じゃあ、このバケツのおよその体積はどうしようか? これも、上面と、下面の半径をそろえて、 こういう円柱に直すと求めやすいね! 3768㎤教え方2 直方体や立方体の体積を計算で求める方法に気づかせ、体積を求める公式を教えます。 問題 下の直方体の体積を計算で求めましょう。 上の直方体の体積を計算で求めるには、下の図を見て下さい。 1だん目の体積を見ると、1辺が1cmの立方体が
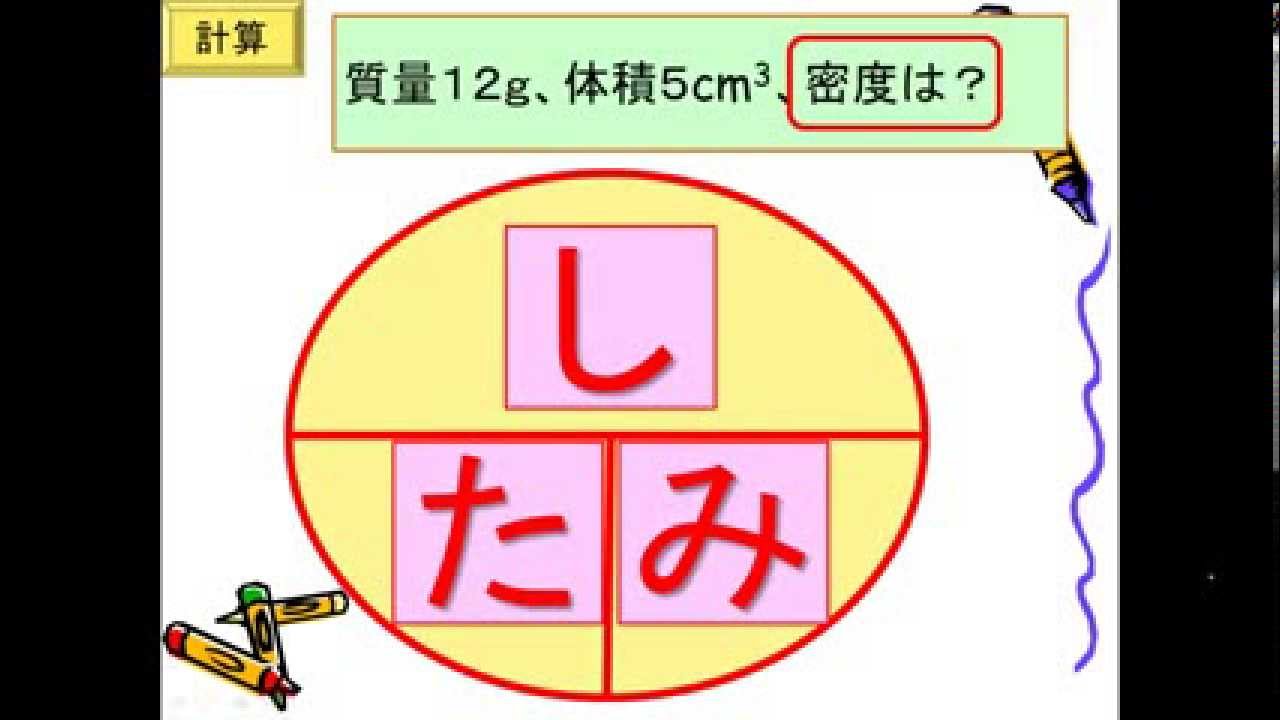



密度の計算 Youtube
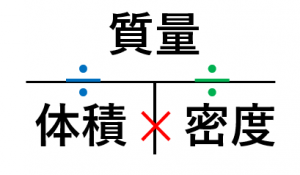



最も共有された 中1 理科 密度 シモネタ
密度の求め方や体積,質量の意味がわかりません。 このようなお悩みをもつ保護者のかたは多いのではないでしょうか? \そんな保護者のかたにおすすめなのが/ ベネッセ教育情報サイト公式アプリ まなびの手帳 お子 縦8cm×横12cm×高さ4cmの直方体の体積から1辺が4cmの立方体の体積を引いても、求めることが出来ます。 直方体の体積=8×12×4=384(cm³)、1辺が4cmの立方体の体積=4×4×4=64(cm³)であることから 求める立体の体積=384-64=3(cm³)となります。 答




3分で分かる 円錐の体積 表面積の求め方をわかりやすく 合格サプリ



中1理科 密度の求め方3パターンの計算方法 Examee




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



定期テスト対策問題 密度の計算 Examee




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




中1理科 密度の計算のコツ 映像授業のtry It トライイット




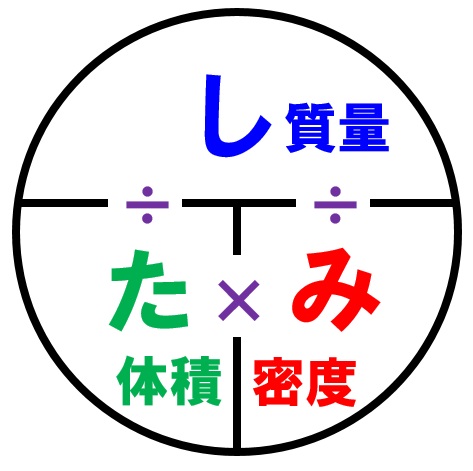
密度の公式 覚え方は し み た でバッチリ 中学数学 理科の学習まとめサイト



中1理科 密度の求め方3パターンの計算方法 Examee



中1化学 質量と重さ 体積 中学理科 ポイントまとめと整理




密度の計算と 溺れないためにできること Menon Network




中学理科 計算問題 密度を求める問題 Youtube




物質 気体 水溶液 密度はどのように求めるのか 中学理科 定期テスト対策サイト




中1理科 密度は公式を忘れても解ける 密度 体積 質量 Youtube
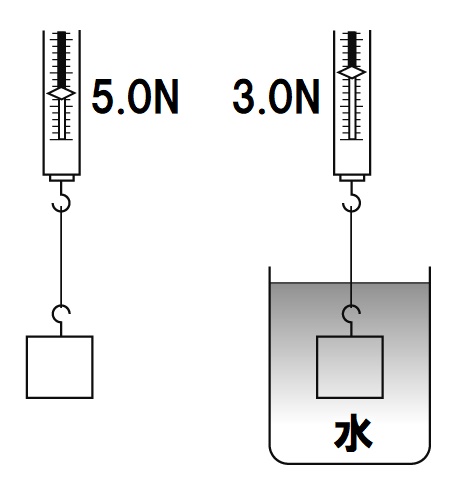



中1理科 浮力の求め方4パターンの計算方法 Examee




理科 中1 31 状態変化するときの体積と質量 Youtube




小中学理科編 物質のようす 体積 重さ 密度について 前編 はまるとんチャンネル




理科 中1 19 密度の計算 Youtube




中学理科 3分でわかる 密度の求め方 出し方の計算公式 Qikeru 学びを楽しくわかりやすく
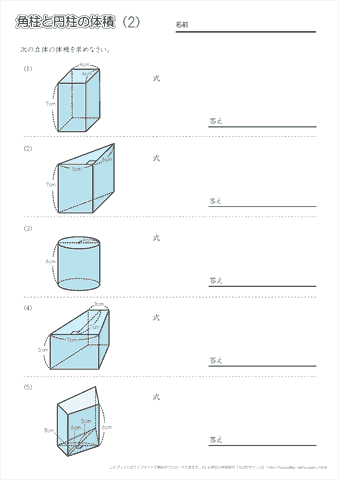



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ



3



質量の求め方は 1分でわかる公式と求め方 体積 密度との関係 求め方
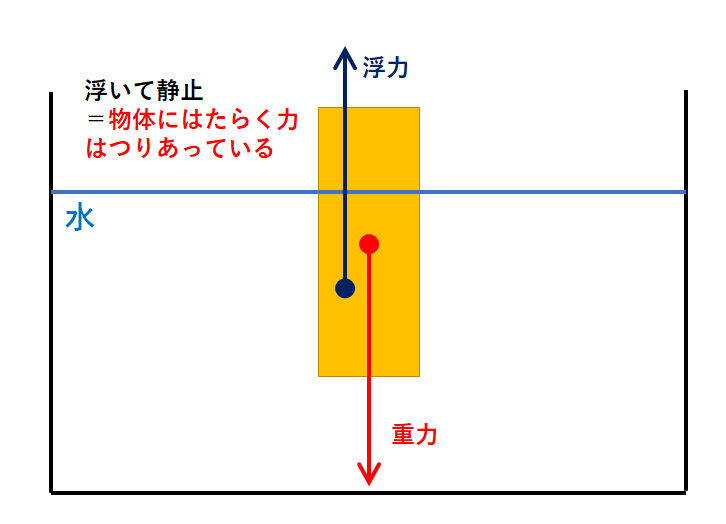



中1物理 浮力の計算 中学理科 ポイントまとめと整理




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



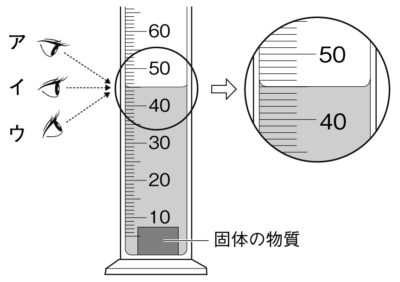
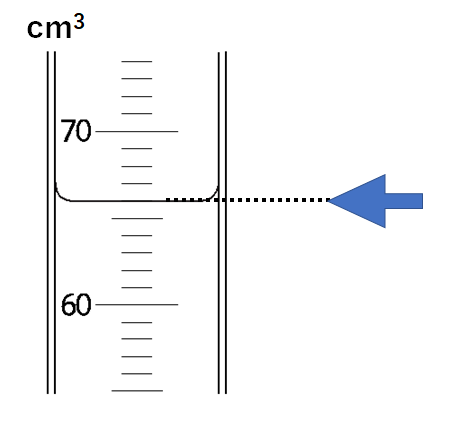
メスシリンダー
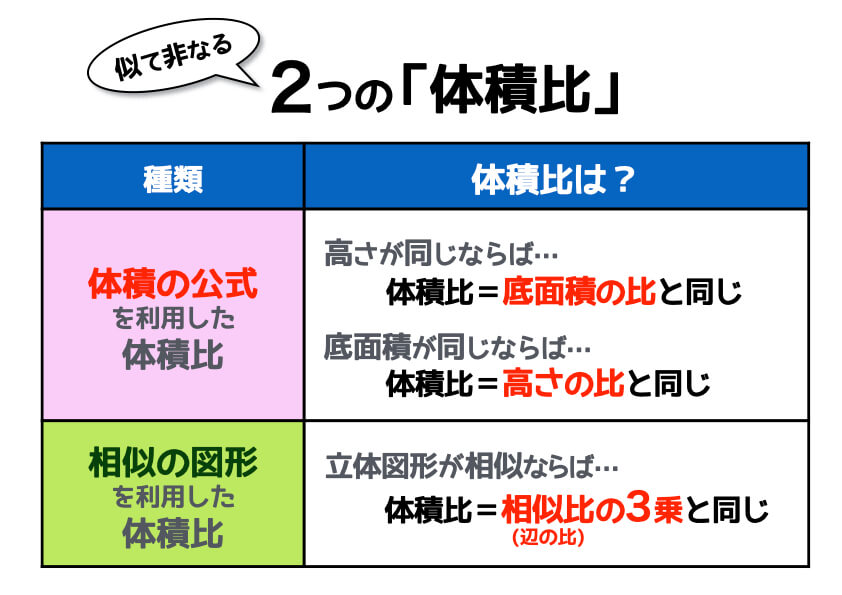



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




物質量の求め方とは 単位や計算問題も解説 高校生向け受験応援メディア 受験のミカタ
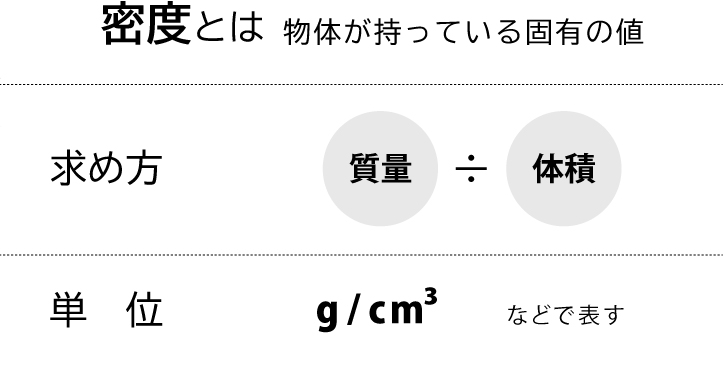



入試理科の注目のワード 密度 を理解する なるほどなっとく 中学受験理科 中学受験ナビ




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




浮力とは 計算問題をさくっと解くための公式とポイントを解説します のぼゆエンジニアリング




密度の公式 物質の密度の求め方は しみた の法則 中学理科 Yattoke 小 中学生の学習サイト
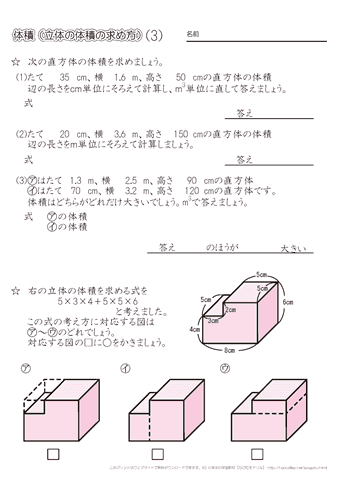



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



中1です 理科についてなんですが 質量を求める公式と 体積を求める公式を教 Yahoo 知恵袋



中学校理科の公式一覧
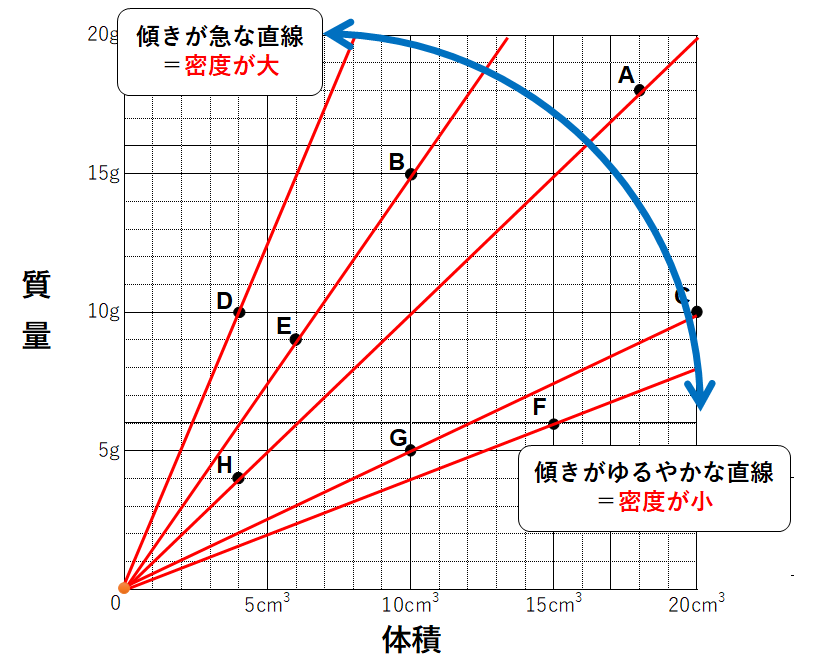



中1化学 密度 中学理科 ポイントまとめと整理



浮力の公式や求め方が読むだけでわかる
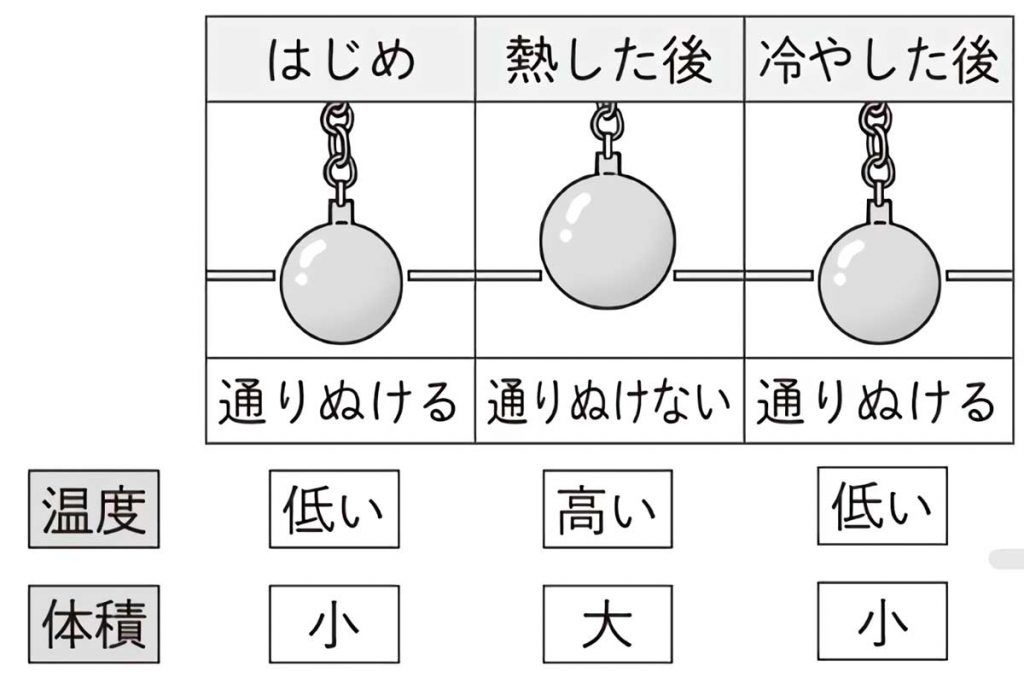



小4理科 ものの温度と体積 指導アイデア みんなの教育技術




中1理科 密度と体積 練習編3 映像授業のtry It トライイット




中1理科 密度の計算 練習編1 映像授業のtry It トライイット



3



密度と体積の関係は 1分でわかる意味 違い 計算と覚え方 質量との関係




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




中1理科 密度の表し方 映像授業のtry It トライイット



5年生カテゴリの記事一覧 翁島 おきなしま 小学校ホームページ




中1 理科 1 質量と密度 Youtube




中学理科 密度の定期テスト予想問題 Pikuu
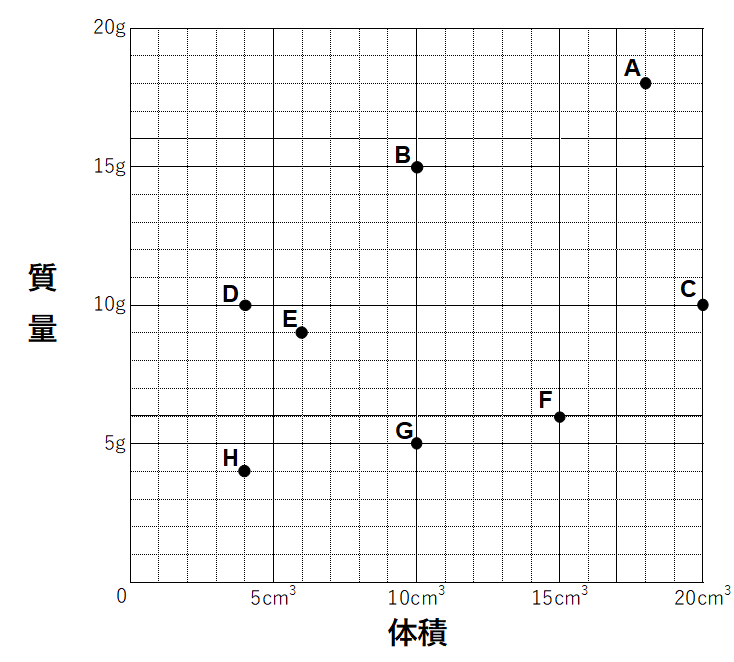



中1化学 密度 中学理科 ポイントまとめと整理
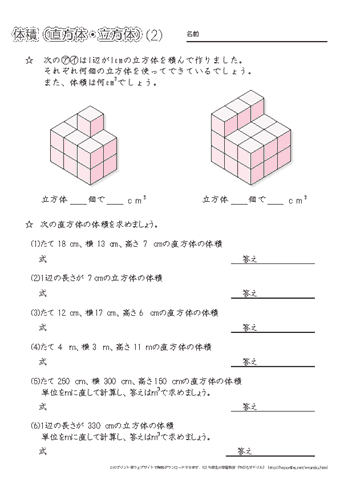



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




中1理科 密度の計算 3パターンの計算方法 Pikuu
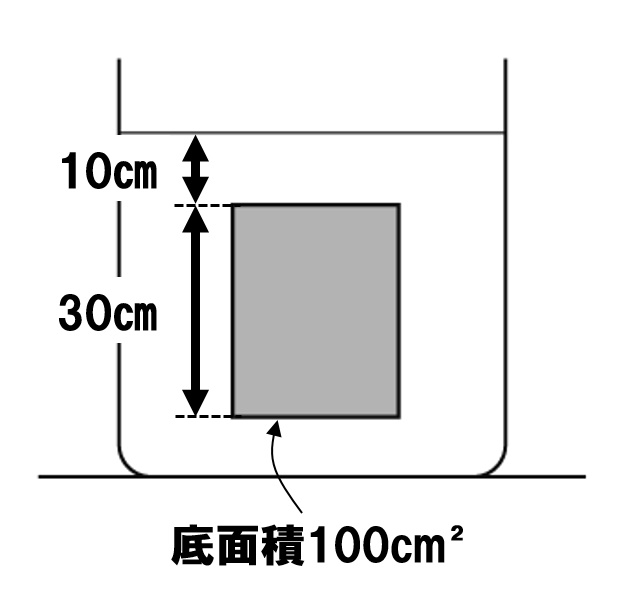



中1理科 浮力の求め方4パターンの計算方法 Examee




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




中学理科 3分でわかる 密度の求め方 出し方の計算公式 Qikeru 学びを楽しくわかりやすく
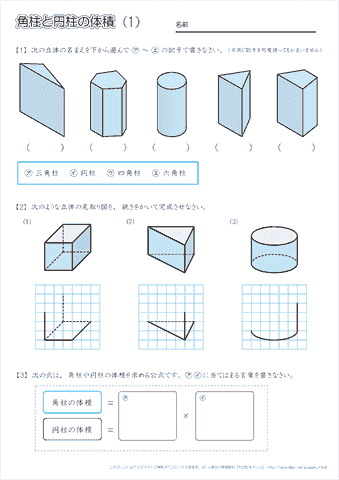



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
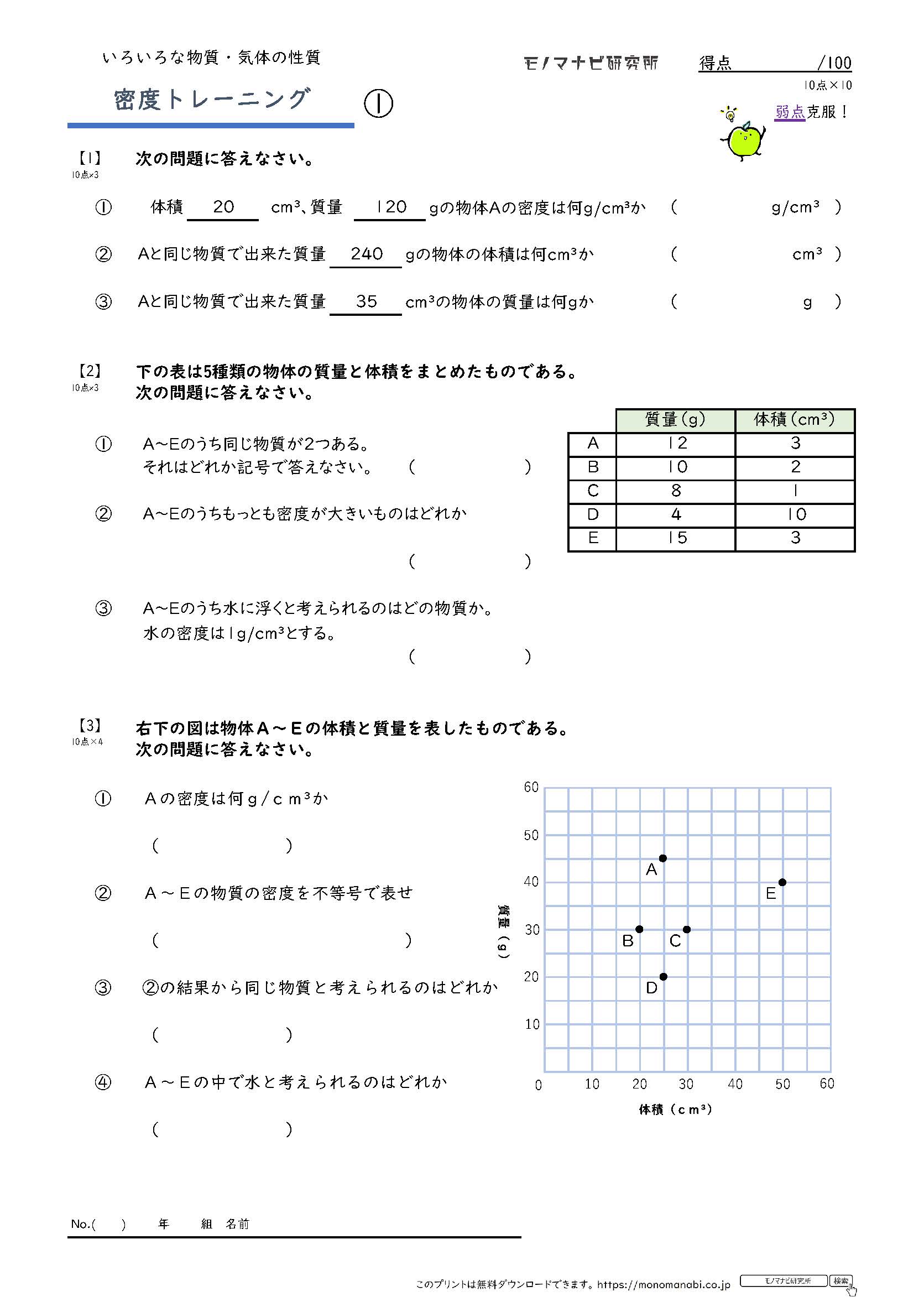



モノマナビ研究所



練習3 密 度 1年理科 化学 Takaの授業記録12
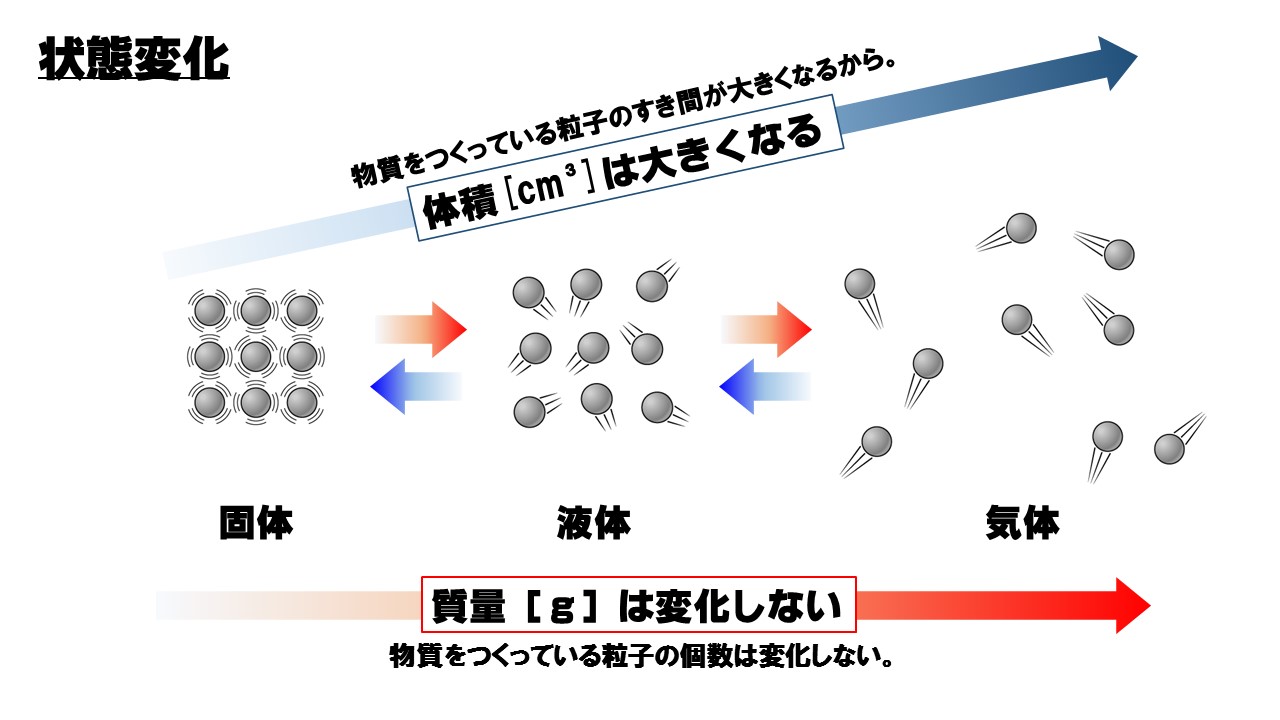



中1理科 状態変化と質量 体積 密度のポイント Examee




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
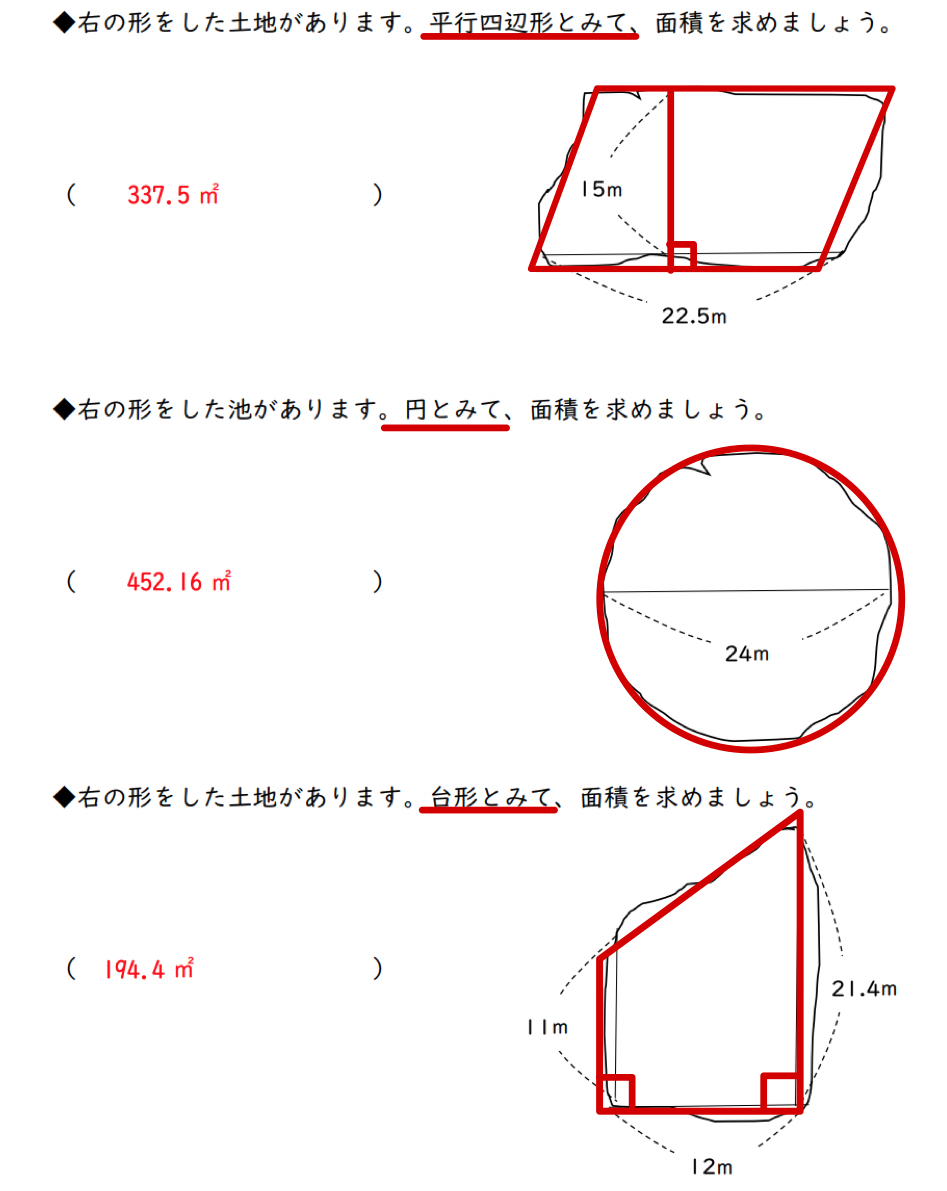



小6算数 およその面積と体積 学習プリント 練習問題 無料ダウンロード印刷




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




意味や単位をおさらい 質量 体積 密度 について元塾講師が解説 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン
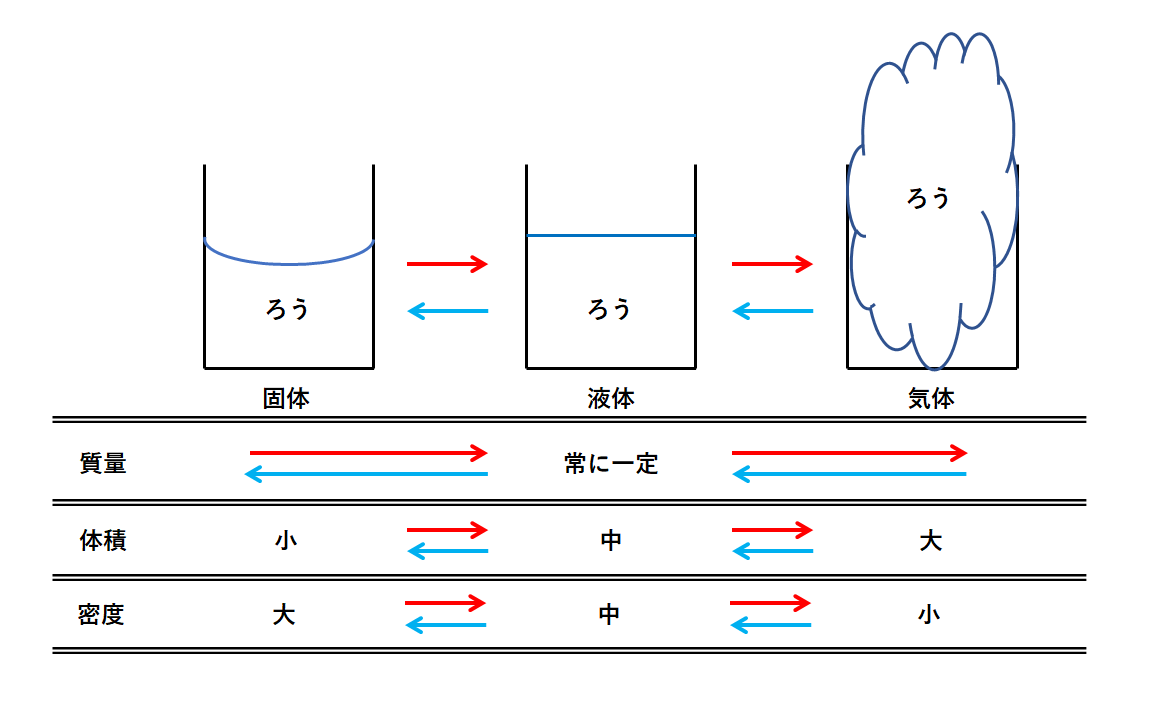



中1化学 状態変化 中学理科 ポイントまとめと整理
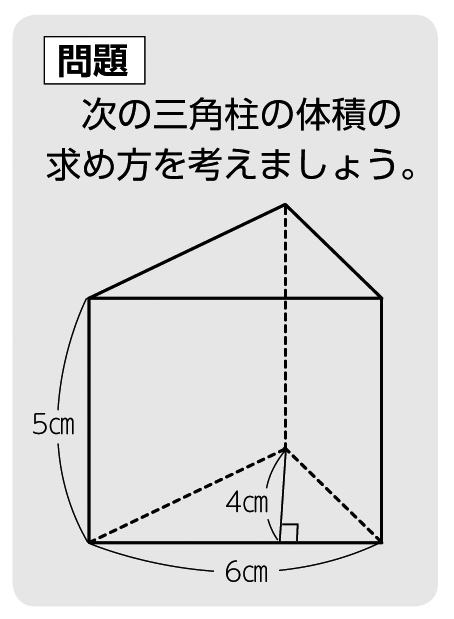



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術
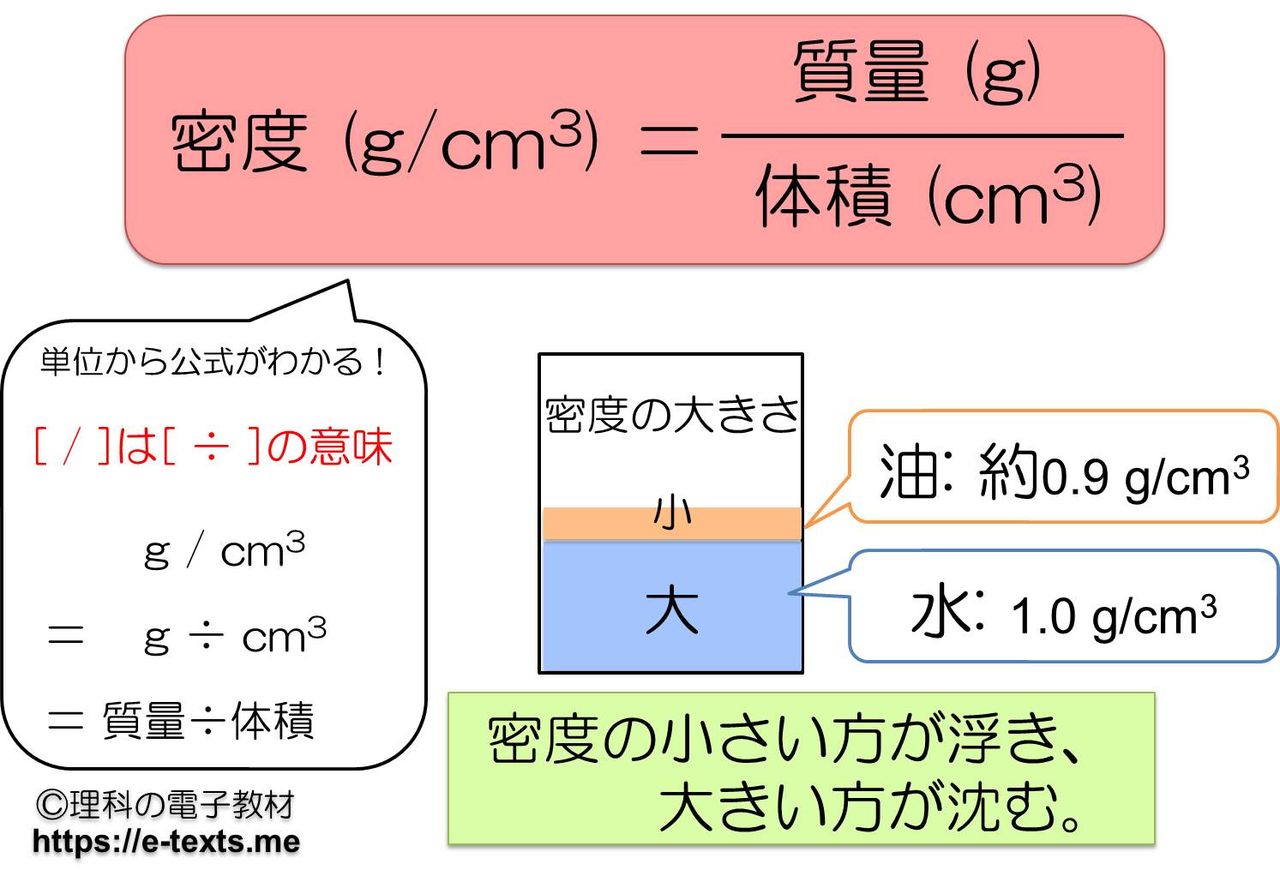



中1化学 密度 Hiromaru Note
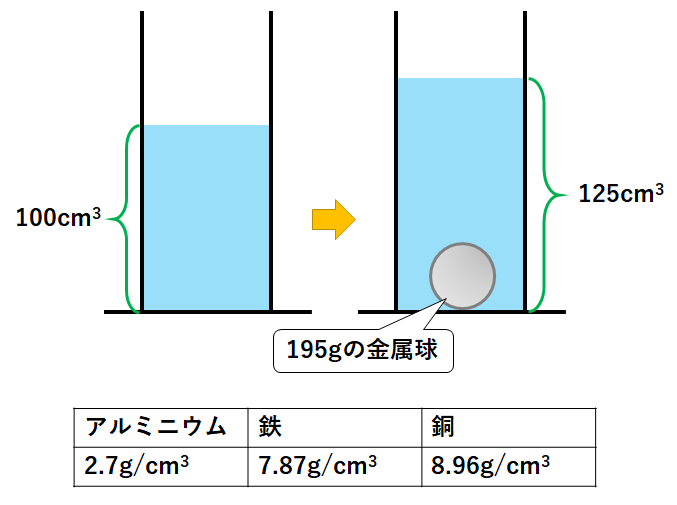



中1化学 密度から物体を推定する実験 中学理科 ポイントまとめと整理




いろいろな物質と密度 無料で使える中学学習プリント




どうして1 3なの 錐の体積の公式の求め方 まなべーと
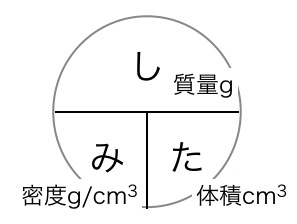



密度の式を はじき みやじ 形式で覚える しみた 理科 科学のネタ帳




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




固体 液体 気体 状態変化で体積 密度はどのように変わる 中学数学 理科の学習まとめサイト




中1理科 密度の計算 映像授業のtry It トライイット




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
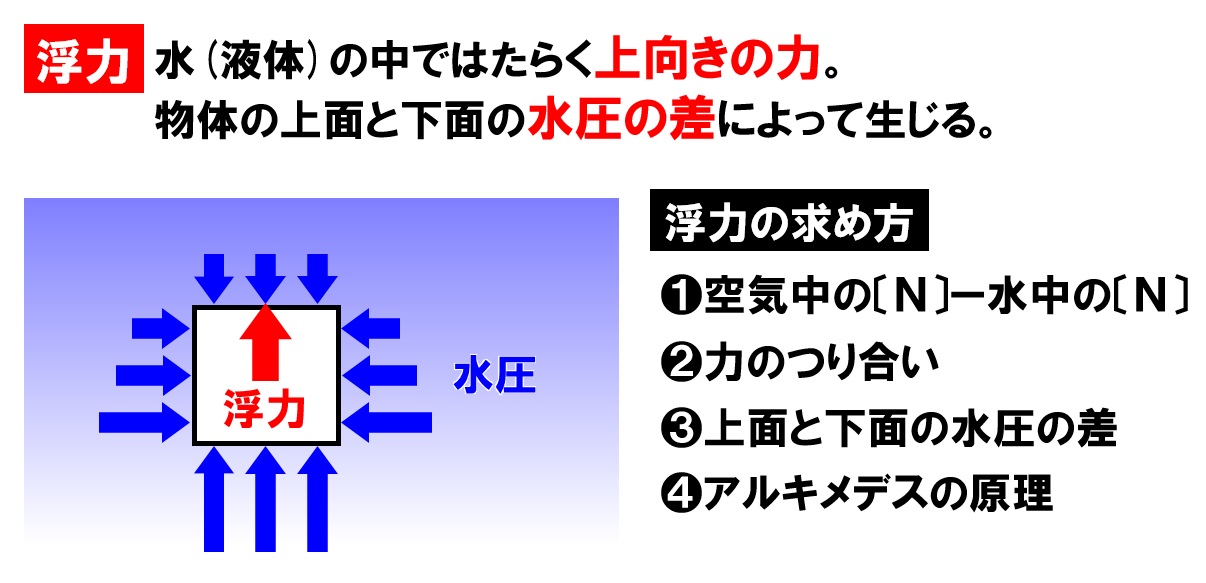



中1理科 浮力の求め方 アルキメデスの原理などの計算方法 Pikuu




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




中学理科 3分でわかる 密度の求め方 出し方の計算公式 Qikeru 学びを楽しくわかりやすく
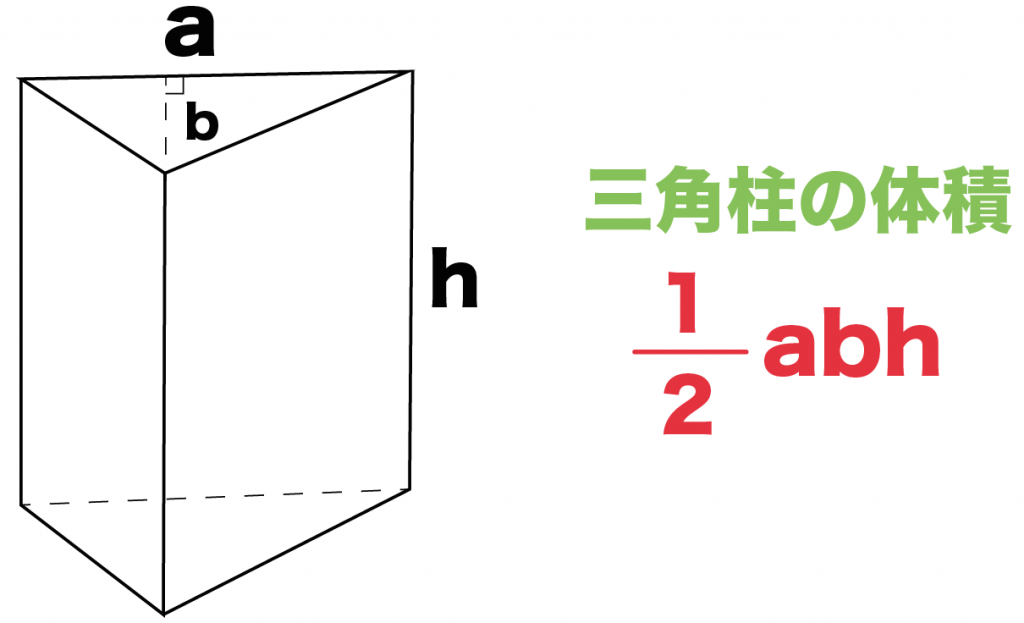



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




メスシリンダーの読み方 見方 使い方の手順などを解説 中学理科のポイントまとめ 中学数学 理科の学習まとめサイト
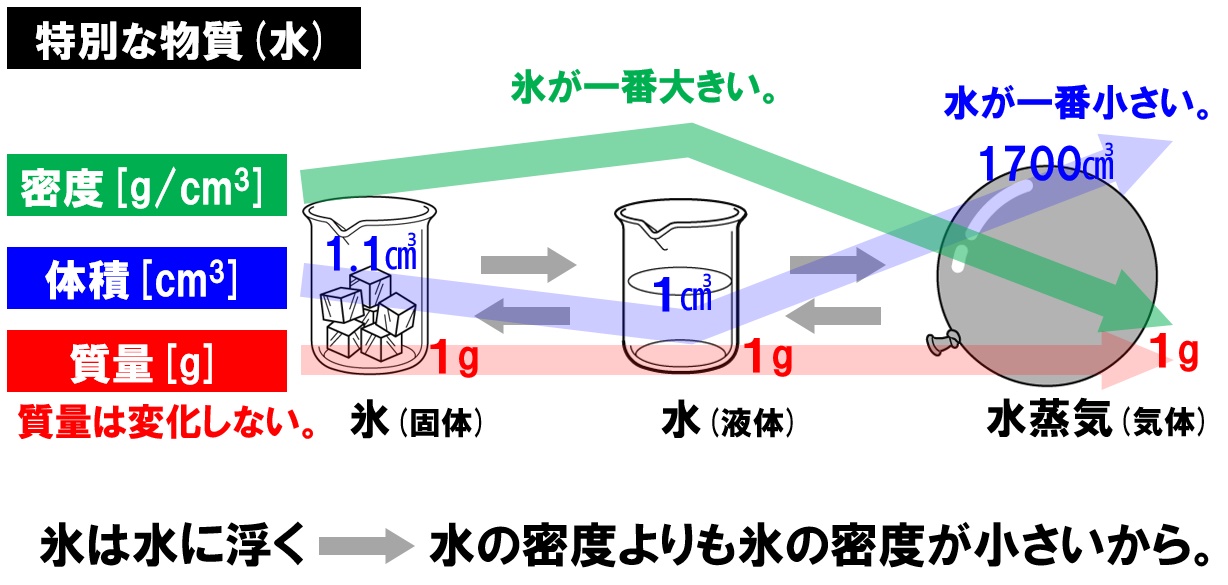



中1理科 状態変化 質量 体積 密度の変化 Pikuu




中1理科 密度の求め方の要点まとめノート デルココ




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
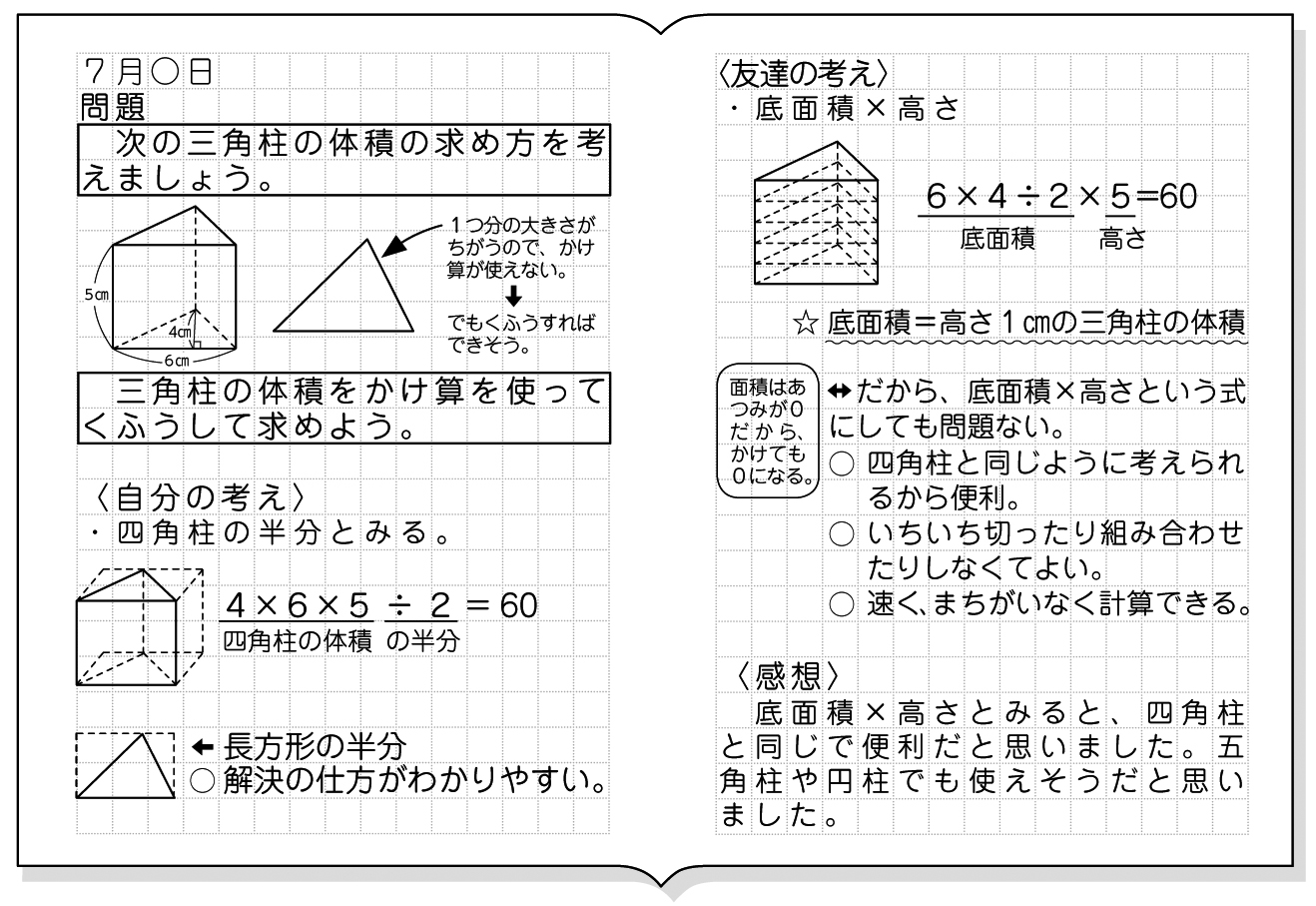



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術




密度の公式 覚え方は し み た でバッチリ 中学数学 理科の学習まとめサイト
コメント
コメントを投稿